При решении многих практических задач не всегда нужно характеризовать случайную величину полностью, т. е. определять законы распределения. Кроме того, построение функции или ряда распределений для дискретной, а плотности - для непрерывной случайной величины громоздко и излишне.
Иногда достаточно указать отдельные числовые параметры, частично характеризующие особенности распределения. Необходимо знать некоторое среднее значение каждой случайной величины, около которого группируется ее возможное значение, или степень разбросанности этих значений относительно среднего и т. п.
Характеристики наиболее существенных особенностей распределения называются числовыми характеристиками случайной величины. С их помощью облегчается решение многих вероятностных задач без определения для них законов распределения.
Важнейшей характеристикой положения случайной величины на числовой оси является математическое ожидание М [X ] = а, которое иногда называется средним значением случайной величины. Для дискретной случайной величины X с возможными значениями x 1 , x 2 , … , x n и вероятностями p 1 , p 2 ,… , p n его определяют по формуле
Учитывая, что =1, можно записать
Таким образом, математическим ожиданием дискретной случайной величины называется сумма произведений возможных ее значений на их вероятности. Среднее арифметическое значение наблюдаемых значений случайной величины при большом числе опытов приближается к ее математическому ожиданию.
Для непрерывной случайной величины X математической ожидание определяется не суммой, а интегралом
где f (x ) - плотность распределения величины X.
Математическое ожидание существует не для всех случайных величин. Для некоторых из них сумма, или интеграл, расходится, и, следовательно, математического ожидания не существует. В этих случаях по соображениям точности следует ограничивать область возможных изменений случайной величины X, для которых сумма, или интеграл, будут сходиться.
На практике применяются и такие характеристики положения случайной величины, как мода и медиана.
Модой случайной величины называется ее наиболее вероятное значение. В общем случае мода и математическое ожидание не совпадают.
Медианой случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины , т. е. это абсцисса точки, в которой ограниченная кривой распределения площадь делится пополам. Для симметричного распределения все три характеристики совпадают.
Кроме математического ожидания, моды и медианы в теории вероятностей используются и другие характеристики, каждая из которых описывает определенное свойство распределения. Например, числовыми характеристиками, характеризующими рассеивание случайной величины, т. е. показывающими, насколько тесно сгруппированы ее возможные значения около математического ожидания, являются дисперсия и среднее квадратическое отклонение. Они существенно дополняют случайную величину, так как в практике часто встречаются случайные величины с равными математическими ожиданиями, но различными распределениями. При определении характеристик рассеивания используют разность между случайной величиной X и ее математическим ожиданием, т. е.
где а = М [X ] - математическое ожидание.
Эта разность называется центрированной случайной величиной, соответствующей величине X, и обозначается :
Дисперсия случайной величины - это математическое ожидание квадрата отклонения величины от ее математического ожидания, т. е.:
D[X ]=M[(X – a ) 2 ], или
D[X ]=M[ 2 ].
Дисперсия случайной величины является удобной характеристикой рассеивания и разбросанности значений случайной величины около ее математического ожидания. Однако она лишена наглядности, так как имеет размерность квадрата случайной величины.
Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такой величиной является среднее квадратическое отклонение случайной величины, которое представляет собой положительный квадратный корень из ее дисперсии .
Математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение - наиболее часто используемые числовые характеристики случайных величин . При решении практических задач, когда невозможно определить закон распределения, приблизительным описанием случайной величины являются ее числовые характеристики, выражающие какое-либо свойство распределения.
Кроме основных характеристик распределения центра (математического ожидания) и рассеивания (дисперсии) часто нужно описать другие важные характеристики распределения - симметрию и островершинность, которые можно представить с помощью моментов распределения.
Распределение случайной величины, полностью задано, если известны все его моменты. Однако многие распределения можно полностью описать с помощью первых четырех моментов, которые являются не только параметрами, описывающими распределения, но имеют также важное значение при подборе эмпирических распределений, т. е. вычислив числовые значения моментов для заданного статистического ряда и, использовав специальные графики, можно определить закон распределения.
В теории вероятностей различают моменты двух видов: начальные и центральные.
Начальным моментом k-го порядка случайной величины Т называют математическое ожидание величины X k , т. е.
Следовательно, для дискретной случайной величины он выражается суммой
а для непрерывной – интегралом
Среди начальных моментов случайной величины особое значение имеет момент первого порядка, который является математическим ожиданием. Начальные моменты высших порядков используются, главным образом, для вычисления центральных моментов.
Центральным моментом k-го порядка случайной величины называют математическое ожидание величины (X - М [X ]) k
где а = М [X].
Для дискретной случайной величины он выражается суммой
а для непрерывной – интегралом
Среди центральных моментов случайной величины особое значение имеет центральный момент второго порядка, который представляет дисперсию случайной величины.
Центральный момент первого порядка всегда равен нулю.
Третий начальный момент характеризует асимметрию (скошенность) распределения и по результатам наблюдений для дискретной и непрерывной случайных величин определяется соответствующими выражениями:
Поскольку он имеет размерность куба случайной величины, то, чтобы получить безразмерную характеристику, m 3 делят на среднее квадратическое отклонение в третьей степени
Полученная величина называется коэффициентом асимметрии и в зависимости от знака характеризует положительную (As > 0) или отрицательную (As < 0) скошенность распределения (рис. 2.3).
71,Числовые характеристики случайных величин широко применяются на практике расчета показателей надежности. Во многих вопросах практики нет необходимости полностью, исчерпывающим образом характеризовать случайную величину. Зачастую бывает достаточно указать только числовые параметры, до некоторой степени характеризующие существенные черты распределения случайной величины, например: среднее значение , около которого группируются возможные значения случайной величины; число, характеризующее рассеяние случайной величины относительно среднего значения, и т. д. Числовые параметры, позволяющие в сжатой форме выразить наиболее существенные особенности случайной величины, называются числовыми характеристиками случайной величины.
а ) б )
Рис. 11 Определение математического ожидания
Числовые характеристики случайных величин, применяемые в теории надежности, приведены в табл. 1.
72,Математическое ожидание
(среднее значение) непрерывной случайной величины , возможные значения которой принадлежат интервалу 
, представляет собой определенный интеграл (рис., 11, б
)
. (26)
Математическое ожидание можно выразить через дополнение интегральной функции. Для этого подставим (11) в (26) и проинтегрируем по частям полученное выражение
, (27)
так как 
и 
, то
. (28)
Для неотрицательных случайных величин, возможные значения которых принадлежат интервалу , формула (28) принимает вид
. (29)
т. е. математическое ожидание неотрицательной случайной величины, возможные значения которой принадлежат интервалу , численно равно площади под графиком дополнения интегральной функции (рис., 11, а
).
73,Средняя наработка до первого отказа по статистической информации определяется по формуле
, (30)
где - наработка до первого отказа i -го объекта; N - число испытываемых объектов.
Аналогично определяется средний ресурс, средний срок службы, среднее время восстановления работоспособности, средний срок сохраняемости .
74,Рассеивание случайной величины около ее математического ожидания оценивается с помощью дисперсии среднего квадратического отклонения (СКО) и коэффициента вариации .
Дисперсия непрерывной случайной величины X представляет собой математическое ожидание квадрата отклонения случайной величины от ее математического ожидания и вычисляется по формуле
. (31)
Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно.
75,Среднее квадратическое отклонение случайной величины является квадратным корнем из дисперсии и имеет размерность случайной величины
. (32)
76,Коэффициент вариации является относительным показателем рассеивания случайной величины и определяется как отношение среднего квадратического отклонения к математическому ожиданию
. (33)
77,Гамма - процентное значение случайной величины
- значение случайной величины , соответствующее заданной вероятности 
того, что случайная величина примет значение, большее ,
. (34)
78,Гамма - процентное значение случайной величины можно определить по интегральной функции, ее дополнению и дифференциальной функции (рис. 12). Гамма-процентное значение случайной величины является квантилем вероятности (рис. 12, а )
. (35)
В теории надежности используется гамма-процентное значение ресурса, срока службы и срока сохраняемости (табл. 1). Гамма-процентным называется ресурс, срок службы, срок сохраняемости, который имеет (и превышает) процентов объектов данного типа.
а ) б )
Рис.12 Определение гамма-процентного значения случайной величины
Гамма-процентный ресурс
характеризует долговечность
при выбранном уровне 
вероятности неразрушения. Гамма-процентный ресурс назначается с учетом ответственности объектов. Например, для подшипников качения наиболее часто используют 90-процентный ресурс, для подшипников наиболее ответственных объектов выбирают 95-процентный ресурс и выше, приближая его к 100-процентному, если отказ опасен для жизни людей.
79,Медиана случайной величины
является ее гамма- процентным значением при 
. Для медианы 
одинаково вероятно, окажется ли случайная величина Т
больше или меньше ее, т. е. .
Геометрически медиана является абсциссой точки пересечения интегральной функции распределения и ее дополнения (рис. 12, б ). Медиану можно истолковать как абсциссу точки, в которой ордината дифференциальной функции делит пополам площадь, ограниченную кривой распределения (рис., 12, в ).
Медиана случайной величины используется в теории надежности как числовая характеристика ресурса, срока службы, срока сохраняемости (табл. 1).
Между показателями надежности объектов существует функциональная связь. Знание одной из функций 
позволяет определить другие показатели надежности. Сводка соотношений между показателями надежности приведена в табл. 2.
Таблица 2. Функциональная связь между показателями надежности
«Единицы измерения физических величин» - Абсолютная погрешность равна половине цены деления измерительного прибора. Микрометр. Результат получают непосредственно при помощи измерительного прибора. Длина коробка: 4 см с недостатком 5 см с избытком. Для каждой физической величины имеются соответствующие единицы измерения. Часы. Относительная погрешность.
«Величины длины» - 2. Какие величины можно сравнить между собой: 2. Объясните, почему следующая задача решается при помощи сложения: 2. Обосновать выбор действия при решении задачи. Сколько получилось пакетов? Сколько ручек в трех таких коробках? Из 12 м ткани сшили платья, расходуя на каждое по 4 м. Сколько платьев сшили?
«Физические величины» - Границы, разделяющие физику и другие естественные науки, исторически условны. Результат всякого измерения всегда содержит некоторую погрешность. Новая тема. Скорость. Взаимодействие тел. Физические законы представляются в виде количественных соотношений, выраженных на языке математики. Погрешность измерений.
«Число как результат измерения величины» - «Число как результат измерения величины» урок математики в 1 классе. Измерение длины отрезка с помощью мерки.
«Числа и величины» - Знакомство с понятием массы. Сравнение масс без измерений. Римская письменная нумерация. Вместимость. Ученик научится: Числа и величины (30 часов) Координатный луч Понятие о координатном луче. Планируемые предметные результаты по разделу «Числа и величины» во 2 классе. Общий принцип образования количественных числительных в пределах изученных чисел.
«Величина спроса» - Причины изменения спроса. Полученная на графике кривая DD (от англ. demand – "спрос") называется кривой спроса. Эластичный спрос (Еpd>1). Величина спроса. Факторы влияющие на спрос. Зависимость величины спроса от уровня цены называется шкалой спроса. Абсолютно неэластичный спрос (Еpd=0).
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):
(6б
)
Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
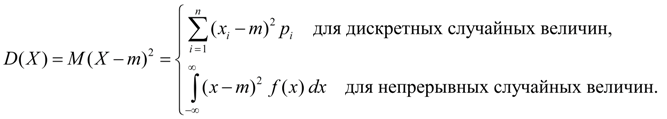(9)
Здесь m = М (Х ).
Свойства дисперсии:
Среднее квадратичное отклонение:
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:
(12)
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
(13)
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
(14)
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С
ее центр распределения сдвигается на то же значение С
, а отклонение от центра не меняется: Х
– m
= (Х
– С
) – (m
– С
).
Теперь очевидно, что дисперсия
– это центральный момент второго порядка
:
Асимметрия. Центральный момент третьего порядка:
(17)
служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :
(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
Рис. 2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
(19)
служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:
(20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода
дискретной
случайной величины – это ее наиболее вероятное значение. Модой
непрерывной
случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным
. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным
. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными
. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального
, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.
